Universitatea Politehnica Timişoara Facultatea de Automatică şi Calculatoare Secţia Calculatoare

LUCRARE DE DIPLOMĂ

- rezumat -

Verificator Flexibil şi Extensibil

Implementat în Java

(jFlexCheck)

Candidat: Andrei FIROIU

Conducător Ştiinţific: Conf. Dr. Marius MINEA

- Sesiunea iunie 2003 –

I. Enunţul temei

Proiectul îşi propune implementarea unui verificator structurat pe concepte fundamentale generice (mulţimi de stări, tranziţii, paşi de explorare înainte şi înapoi), şi permiţând instanţierea lor, într-o ierarhie de clase, cu reprezentări şi metode specifice. Un mic limbaj de comenzi va permite utilizatorului scrierea de algoritmi pornind de la operaţiile elementare disponibile. Sistemul va putea fi folosit ca platformă pentru evaluarea rapidă a performanţei unor noi reprezentări sau algoritmi.

II. Prezentare generală

Metode formale

Sistemele hardaware şi software cresc continuu şi inevitabil în timp ca mărime şi complexitate. Datorită acestei creşteri probabilitatea apariţiei unor erori subtile şi nedetectabile creşte şi ea. Mai mult decât atât, în unele aplicaţii critice, apariţia unor astfel de erori poate duce la importante pierderi materiale şi chiar de vieţi omeneşti. Din această cauză, un scop major în Ingineria Software este găsirea unor metode de dezvoltare a unor sisteme viabile, independent de mărimea acestora. O categorie de astfel de metode o constituie metodele formale, ce pot fi definite ca limbaje tehnici şi metode matematice pentru specificarea şi verificarea sistemelor. Folosirea acestor metode nu oferă garanţii absolute. Metodele formale depind foarte mult de modelul şi specificaţiile folosite. Cu toate acestea, cu ajutorul lor se pot descoperi inconsistenţe, ambiguităţi şi lipsuri în sistem, care altfel ar fi putut trece neobservate. În plus, folosind metodele formale, procesul de testare poate fi automatizat, acest lucru ducând la creşterea performanţei şi corectitudinii sistemelor.

În Figura 1 este prezentată utilizarea metodelor formale pe întreg parcursul ciclului de producţie.

Două dintre cele mai importante tehnici de verificare formală sunt model checking şi theorem proving. Tema lucrării se încadrează în tehnicile de model checking, de aceea în continuare ne vom concentra doar pe acest domeniu.

Model checking

Model checking este o tehnică de verificare automată pentru sisteme concurente cu stări finite, cum ar fi de exmplu plăcile de circuite secvenţiale sau protocoalele de comunicaţie. Comparativ cu alte tehnici, metoda model checking se bucură de două mari avantaje:

· Este complet automată şi nu necesită supraveghere din partea unor specialişti sau experţi în discipline matematice, aşa cum este nevoie în cazul metodei theorem proving.

· Când sistemul nu reuşeşte să satisfacă o anumită cerinţă, procesul de model checking va genera întotdeauna un contraexemplu care va demonstra respectiva încălcare a cerinţei.

Analiza cerinţelor	- identifică contradicţii, ambiguităţi, omisiuni
Proiectare	- descompunerea în componente şi specificarea interfeţelor
Verificare
Testare şi depanare	- generarea direcţionată de cazuri de test
Analiză	- model abstract, mai puţin complex decât sistemul real

Figura 1. Utilizarea metodelor formale pe întreg parcursul ciclului de producţie.

Tehnica de model checking presupune următoarele etape: modelarea, specificarea şi verificarea sistemului. Modelarea presupune convertirea sistemului într-un formalism accpetat de către un instrument de model checking. Înainte de verificare, este necesar să se specifice proprietaţile ce trebuie îndeplinite de către sistem. Verificarea este procesul prin care se va stabili dacă sistemul îndeplineşte proprietăţile cerute. Teoretic, verificarea este complet automată. În practică, procesul necesită totuşi şi asistenţă umană. O astfel activitate este analiza rezultatelor. În cazul unui rezultat negativ al analizei, utilizatorului i se va furniza o „istorie” a erorii. În acest caz, eroarea trebuie identificată şi asupra sistemului se vor opera modificările necesare, după care algoritmul de model checking va fi repornit.

III. Prezentarea lucrării

Aplicaţia este structurată în trei module fundamentale:

A. Compilatorul pentru limbajul în care se vor scrie algoritmii.

Sistemul de tipuri al limbajului suportă tipuri primare întreg şi boolean, cât şi tipurile complexe subrange (interval de întregi) şi enumerare. Expresiile, constantele şi variabilele sunt puternic tipizate.

Principala entitate a limbajului este modulul. De obicei, un sistemul este descris ca şi un modul sau ca o compoziţie de mai multe module. Un modul poate fi parametrizat şi este compus dintr-o mulţime de stări şi din tranziţiile între aceste stări. O stare este definită prin intermediul a două seturi de variabile - de intrare (variabile observate) şi de ieşire (variabile controlate). Tranziţia într-o stare nouă, este controlată printr-o condiţie exprimată în variabilele ce definesc respectiva stare. Compoziţia modulelor poate fi serială sau paralelă (asincronă). Există reguli ce guvernează utilizarea variabilelor într-o compoziţie de module. Două module dintr-o compoziţie nu trebuie să partajeze aceleaşi variabile de ieşire. Modulele pot partaja variabile de intrare şi de asemenea, variabilele de intrare ale unui modul pot fi variabilele de ieşire ale celuilalt. Operaţiile cu module mai includ redenumirea de variabile şi ascunderea de variabile. Prima operaţie este necesară pentru evitarea de conflicte între variabile într-o compoziţie, în timp ce a doua este necesară în cazul în care se doreşte folosirea unei variabile ca şi variabilă privată într-un modul.

Figura 2 prezintă un program scris în limbajul jFlexCheck, iar în Figura 3 se poate urmări reprezentarea grafică a stărilor şi tranziţiilor sistemului.

system : MODULE =

BEGIN

OUTPUT

pc1, pc2 : {trying,critical},

semaphore : BOOLEAN

INITIALIZATION

pc1 = trying;

pc2 = trying;

semaphore = TRUE

TRANSITION

[

(pc1=trying) AND semaphore -->

pc1' = critical;

semaphore' = FALSE

[]

pc1=critical -->

pc1' = trying;

semaphore' = TRUE

[]

(pc2=trying) AND semaphore -->

pc2' = critical;

semaphore' = FALSE

[]

pc2=critical -->

pc2' = trying;

semaphore' = TRUE

]

END;

Figura 2. Exemplu de program scris în jFlexCheck.

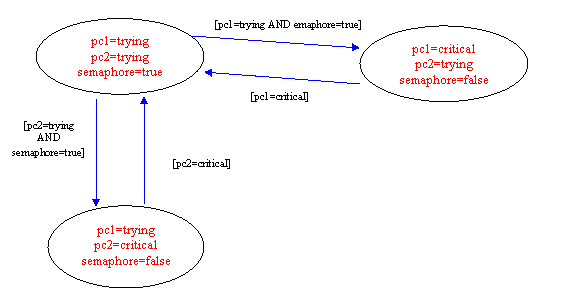
Figura 3. Reprezentarea grafică a stărilor sistemului descris în Figura 2.

B. Modulul pentru construirea modelului sistemului.

Din arborele sintactic abstract generat cu JavaCC, se va construi apoi modelul sistemului sub forma unei structuri Kripke (model ce va fi folosit ulterior pentru model checking). O structură Kripke se defineşte ca un automat cu stări finite, etichetat:

M=(S, , R, L)

unde:

· S: mulţime finită de stări;

· : mulţimea stărilor iniţiale;

· : relaţie de tranziţie totală: (din orice stare există cel puţin o tranziţie);

· : funcţie de etichetare a stărilor (AP = mulţime de propoziţii atomice).

Pentru acest model se pot folosi mai multe reprezentări. În această lucrare au fost implementate două reprezentări: o reprezentare explicită şi o reprezentare prin BDD-uri (binary decision diagrams) – reprezentare de funcţii booleane prin intermediul grafurilor aciclice. Ierarhia de clase pentru reprezentarea modelului a fost astfel proiectată încât să permită extinderea ulterioară cu alte reprezentări, după cum se poate observa în Figura 4.

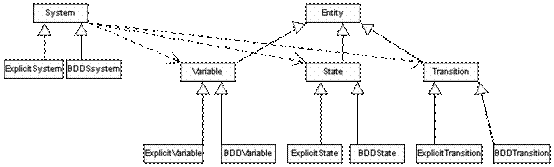
Figura 4. Ierarhia de clase pentru diferitele reprezentări ale sistemului.

C. Algoritmii pentru verificarea modelului.

Pentru verificarea sistemului, cerinţele pe care acesta trebuie să le îndeplinească vor fi exprimate în logică temporală. Logica temporală este un formalism folosit pentru a descrie secvenţe de tranziţii între stările unui sistem reactiv. Există mai multe tipuri de logică temporară, în funcţie de operatorii pe care îi pun la dispoziţie şi de semantica acestora. În această lucrare ne vom concentra pe un tip important de logică temporală, numit .

Conceptual, formulele descriu proprietăţi ale arborilor de computaţie. Un arbore de computaţie arată toate căile posibile de execuţie pornind din starea iniţială. În logica , formulele sunt compuse din operatori temporali şi cuantificatori de cale. Cunatificatorii de cale sunt folosiţi pentru a descrie structurile de ramnificaţie în arborii computaţionali.

Există doi astfel de cuantificatori: A („pentru toate căile de execuţie”) şi E („pentru unele căi de execuţie”). În plus, există cinci operatori de bază: X („next time”); F („in the future”); G („globally”/”always”); U („until”); R („release”).

Cu ajutorul acestor formule, se pot descrie specificaţii complexe pentru un anumit sistem:

· AG (Req AF Ack) : Dacă o apare o cerere, cândva în viitor se va primi şi un semnal de confirmare.

· AG(AFDeviceEnabled) : Propoziţia DeviceEnabled este adevărată de un număr infinit de ori pe fiecare cale de execuţie.

· AG(EF Reset) : Din orice stare este posibil să se ajungă în starea de Reset.

Pe baza acestor formule se vor implementa algoritmii de explorare a stărilor sistemului. Dacă aceste formule sunt verificate, sistemul este considerat corect.

IV. Concluzii

Metodele de verificare bazate pe explorarea automată a tuturor stărilor şi execuţiilor unui model folosesc, în funcţie de optimizările necesare, o mare varietate de reprezentări şi algoritmi. Concepţia lucrării permite adăugarea ulterioară a unor noi tipuri de reprezentări (spre exemplu o reprezentare mixtă – şi explicită şi BDD). De asemenea, algoritmii de parcurgere pot fi îmbunătăţiţi sau noi algoritmi pot fi adăugaţi.

Pe baza acestui tool se pot construi alte sisteme de verificare mai complexe.

V. Referinţe

1. EDMUND M. CLARK, JR., ORNA GRUMBERG, DORON A. PELED – Model Checking. 1999, The MIT Press.

2. EDMUND M. CLARK, JEANNETTE M. WING - Formal Methods: State of the Art and Future Directions. 1998, Carnegie Mellon University.

3. RANDAL E. BRYANT – Symbolic Boolean Manipulation with Ordered Binary Decision Diagrams. 1992, Fujitsu Laboratories, Ltd

4. JOOST-PIETER KATOEN - Concepts, Algorithms and Tools for Model Checking. 1999, Lectures Notes at Friederich-Alexander Univeristy, Erlangen-Nurenberg.